Joint Probability Mass Function
The joint probability mass function (joint PMF) to handle simultaneous calculations of random variables \(X\) and \(Y\) can be expressed as
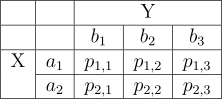
- \(X = \{a_{1}, a_{2}, ..., a_{m}\}\)
- \(Y = \{b_{1}, b_{2}, ..., b_{n}\}\)
- \(p_{ij} = P(X = a_{i}, Y = b_{j})\)
- Each probability is between zero and one inclusively \[0 \leq p_{ij} \leq 1\]
- All probabilities add up to 100 percent \[\displaystyle\sum_{i = 1}^{m}\sum_{j = 1}^{n} p_{ij} = 1\]
- Aside: it is okay if the total is 0.99 or 1.01 (artifact of rounding errors)
Setting
The setting for the examples in this lecture is The Lantern—our beloved coffee shop.

- \(X\): number of beverages purchased by a customer
- \(Y\): number of snacks purchased by a customer

Joint Probability

What is the probability that a randomly selected customer purchased one beverage and one snack?
Marginal Probability Mass Functions
The marginal probability mass functions with respect to \(X\) and \(Y\) respectively are
\[{\color{blue}p_{X}(a_{i}) = \displaystyle\sum_{j = 1}^{n} p(a_{i}, b_{j})}, \quad {\color{red}p_{Y}(b_{j}) = \displaystyle\sum_{i = 1}^{m} p(a_{i}, b_{j})}\]
In our example setting, we have the following joint PMF with marginal probabilities:

More succinctly, the marginal probability mass function of \(X\) is

and the marginal probability mass function of \(Y\) is

What is the probability that a randomly selected customer purchased one beverage or one snack?
Conditional Probability

Compute the probability that a randomly selected customer purchases one snack given that the customer purchased zero beverages.
Compute the probability that a randomly selected customer purchases a beverage given that the customer purchased two snacks.
Conditional Expectation
The concept of conditional probability can be extended into the concept of the expected value.
\[\text{E}[{\color{blue}A}| B = b_{j}] = \displaystyle\sum_{i = 1}^{m} {\color{blue}a_{i}} \cdot {\color{red}P(a_{i} | B = b_{j})} = \displaystyle\sum_{i = 1}^{m} {\color{blue}a_{i}} \cdot {\color{red}\displaystyle\frac{P(A = a_{i}, B = b_{j})}{P(B = b_{j})}}\]

What is the expected number of snacks purchased given that a customer purchases one beverage?
Joint Cumulative Distribution Function
As in the univariate case, the multivariate joint cumulative distribution function (joint CDF) is defined similarly as
\[F(a, b) = P(X \leq a, Y \leq b)\]
Looking Ahead
Exam 1 will be on Wed., Mar. 1
- more information in weekly announcements
No lecture session for Math 32:
- Mar 10, Mar 24
